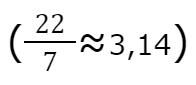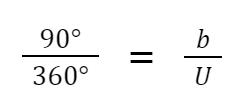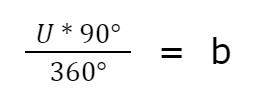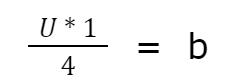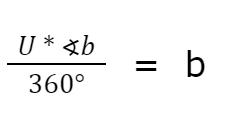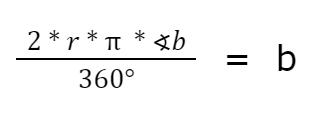Manchmal ist es notwendig , zu wissen , wie lang der Kreisbogen über einem Kreisabschnitt oder Kreissegment ist , hier erklären wir auf möglichst verständliche Art , wie das geht . Mit ein wenig Mathematik (viele werden jetzt stöhnen) ist das relativ einfach zu machen , wir brauchen nur den Radius oder den Durchmesser des Kreises und Größe des Winkels unseres Kreisabschnittes bzw Kreissektors oder Kreisausschnittes …
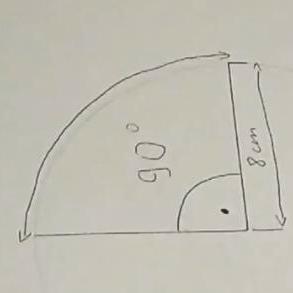
Wir haben einen Kreis , aus dem wir einen Ausschnitt herausnehmen , dessen Kreisbogen wir berechnen wollen .
Unser Abschnitt hat einen Winkel von 90 Grad . Also ein rechter Winkel ,
welcher zugleich ein Viertelkreis ist ,
wie wir bald sehen werden .
Jeder Kreis hat einen Umfang , der vom Radius direkt abhängig ist .
Dieser Kreisumfang berechnet sich aus dem Radius (die Hälfte des Durchmessers) und der Konstante π (Pi) .
Die Formel lautet U = 2 * r * π oder U = d * π wobei π etwa 3,14 entspricht , für alle , die sich 3,14 nicht einfach merken
können als kleine Hilfe : 22 geteilt durch 7 ergibt auch etwa 3,14
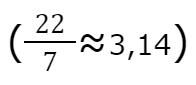 .
.
Der Umfang des ganzen Kreises entspricht 360° , unser Abschnitt hat 90° (analog funktioniert die Berechnung auch mit allen anderen Gradzahlen) .
Wenn wir jetzt den Kreisbogen berechnen wollen , setzen wir unsere 90° , oder wie groß unser Winkel auch ist ,
in Relation zu den 360° des ganzen Kreises :
auf der anderen Seite der Gleichung haben wir dann unser b für den gesuchten Kreisbogen in Relation zum gesamten Kreisumfang U :
b/U so dass unsere Gleichung wie folg aussieht :
| umstellen durch Multiplikation mit U
Durch das Umstellen erhalten wir eine Gleichung mit der gesuchten Länge alleinstehend auf der einen Seite .
| kürzen der Winkel , hier mit 90°
Durch das Kürzen kann die Berechnung einfacher werden , bei 90° ist das der Fall .
Unsere Gleichung sieht nach dem Kürzen wie folgt aus :
Hier sehen wir , dass 90° einem Viertelkreis entsprechen …
Bei anderen Winkeln ergeben sich entsprechend andere Werte im Bruch .
Jetzt können wir die Formel für den Umfang mit integrieren , um eine universelle Berechnungsformel zu erhalten :
Diese Formel verallgemeinern wir zu :
| ∢b ist der Winkel des Kreisausschnittes
Jetzt ersetzen wir U durch die oben stehende Formel
In diese Formel setzen wir jetzt den bekannten Winkel ( ∢b ) sowie der Radius ( r ) ein , kürzen eventuell und erhalten die Länge des Kreisbogens .
Wir haben die Rechnung für einen Winkel von 90° und einen Radius von 8cm ausgeführt , dabei haben wir einen Wert von 12,56cm erhalten . Dann haben wir mit einem biegsamen Stahllineal nachgemessen , unsere Berechnung stimmte , also auch unsere Formel .
Fertig !
VIEEEL BASTELSPASS !!!